线性回归是一种基础而且常用的机器学习算法，顾名思义是一个回归模型。

它的假设是，输出y可以被输入x以线性的方式预测 y = wx + b,

其中，w和b是模型要学习的参数。

线性回归的目标是求解w和b，使得预测输出y与真实输出之间的误差最小。

线性回归的损失函数通常使用均方误差作为衡量指标:

\[MSE = \frac{1}{n} \sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2\]

其中:

  • \(n\) - 样本数量
  • \(Y_i\) - 第\(i\)个样本的真实值
  • \(\hat{Y}_i\) - 第\(i\)个样本的预测值
  • \(\sum\) - 求和符号,对所有样本求和解析:
  • \((Y_i - \hat{Y}_i)\) 表示第\(i\)个样本的预测误差,即真实值与预测值之
  • \((Y_i - \hat{Y}_i)^2\) 对预测误差进行平方,避免正负误差相抵消,误差可能为负也可能为正，取平方有一个特性，它惩罚更大的错误更多。
  • \(\frac{1}{n}\) 求样本平均值,防止样本数量影响所以MSE是每个样本平方误差之和的平均值,反映了模型预测值与真实值的偏差程度。

下面是一个简单的示例，搞明白线性回归是干什么的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np

# 生成数据
# x和y分别是一个一维数组,表示样本的特征和标签
x = np.array([1, 2, 3, 4, 5])
y = np.array([3, 5, 7, 9, 11])

# w和b表示线性模型的参数,初始化为0
w = 0 
b = 0

# lr是梯度下降的学习率,epochs是训练轮数
lr = 0.01 
epochs = 1000

# 训练
for i in range(epochs):
    y_pred = w*x + b #计算预测值   
    loss = np.square(y_pred - y).mean()
    w = w - lr*2/len(x) * np.sum((y_pred - y)*x) 
    b = b - lr*2/len(x) * np.sum((y_pred - y))

print(w, b)

结果

1
2.003880582342283 0.9859898664422495

步骤：

  1. 生成测试数据:x和y数组分别代表输入和输出,这里生成了5个数据点。
  2. 参数初始化:模型参数w和b初始化为0。
  3. 定义超参数:学习率lr为0.01,训练轮数epochs为1000。
  4. 训练:for循环表示进行1000轮训练,每轮都进行以下步骤:
    1. 根据当前参数w和b,计算预测输出y_pred。
    1. 计算损失函数loss,这里使用均方误差。
    1. 根据损失函数求导得出w和b的梯度。
    1. 使用梯度下降算法更新w和b,其中lr是学习率。

​5. 打印出训练后的w和b参数。

分析：

针对这个线性回归代码,最理想的输出结果是:

1
2
w = 2 
b = 1

因为我们生成的示例数据符合这样一个模型:

1
y = 2x + 1

也就是说,真实的模型参数应该是: w(权重参数)= 2 b(偏置参数)= 1

如果模型训练完美,经过足够多的迭代优化,我们期望的参数w和b会收敛到这两个值。

具体来看,在这个代码示例中:

1
2
x = np.array([1, 2, 3, 4, 5])
y = np.array([3, 5, 7, 9, 11])

这些样本点正好符合公式 y = 2x + 1。

所以当代码训练结束后,如果我们的w和b分别收敛到2和1,就说明模型训练是成功的,完美拟合了这个线性关系。

其中调节线性回归模型的学习率会对训练过程和结果产生不同的影响:

  1. 学习率增加:

  • 收敛速度会变快,需要的迭代轮数会减少。

  • 但是容易产生参数的振荡,难以收敛到稳定优化的结果。

  • 最终模型的预测效果可能会变差。

  1. 学习率减小:

  • 收敛速度会变慢,需要更多的迭代轮数。

  • 参数更新会更加稳定和平滑。

  • 最终可以收敛到一个较优的模型,预测效果更好。

  • 但是计算代价更高,需要花费更多时间。

所以学习率的选择需要找到最佳平衡点:

  • 学习率不能太大,否则容易产生参数振荡。

  • 学习率也不能太小,否则收敛速度过慢。

一个通用的方法是从一个较小的学习率开始,如果发现收敛速度过慢,可以适当增加学习率;如果出现振荡,则应该降低学习率。

下面再给出一个较复杂的例子：

这个线性回归的代码示例:

1
2
import numpy as np
import matplotlib.pyplot as plt

导入所需的numpy和matplotlib库。

1
np.random.seed(1)

设置随机数种子,这样可以重现结果。

1
2
x = np.random.uniform(0, 100, 100)
y = 2*x + 3 + np.random.normal(0, 10, 100)

使用numpy随机生成100组训练数据,x范围是0到100,y计算方式是y=2x+3加上正态噪声。

1
2
3
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x.reshape(-1,1), y)

使用scikit-learn中的LinearRegression模型,拟合训练数据x和y。需要reshape x 为二维。

1
2
x_test = np.linspace(0, 100, 100).reshape(-1,1)
y_pred = model.predict(x_test)

生成0-100范围内的100个预测点x_test,用训练好的模型model预测对应的y值,得到y_pred。

1
2
3
4
5
plt.scatter(x, y)
plt.plot(x_test, y_pred, color='r') 
plt.xlabel('x')
plt.ylabel('y')
plt.show()

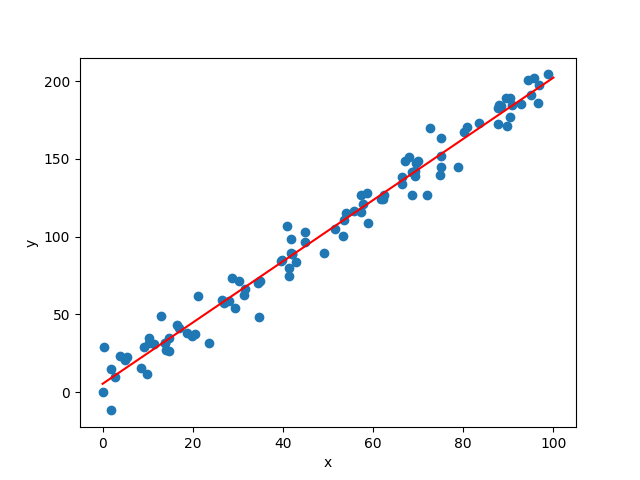
使用matplotlib画出训练数据的散点图,以及用红色线画出预测的线性回归直线。增加坐标标签。

这样我们就可以直观地看到了模型对数据的拟合效果。

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np
import matplotlib.pyplot as plt

# 生成100组随机数据
np.random.seed(1)
x = np.random.uniform(0, 100, 100)
y = 2*x + 3 + np.random.normal(0, 10, 100) 

# 拟合线性回归模型
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x.reshape(-1,1), y)

# 预测
x_test = np.linspace(0, 100, 100).reshape(-1,1)
y_pred = model.predict(x_test)

# 画图
plt.scatter(x, y) 
plt.plot(x_test, y_pred, color='r')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

我们先生成了100组随机数据,其中y满足公式y=2x+3加上一点正态扰动。

然后我们使用scikit-learn中的LinearRegression模型对数据进行线性回归拟合。

最后我们生成100个等间隔的x,用模型预测对应的y,并画出散点图和预测的线性回归直线。

pCIMXMq.png