逻辑回归本质上是一个分类模型,用于预测输入数据属于哪个类别的概率。其基本思想是:

  1. 构建一个线性函数,输入是样本特征,输出是样例属于某类的对数概率。
  2. 将线性函数的输出通过sigmoid函数转换为概率值。
  3. 根据最大概率,对样本进行分类预测。
  4. 通过最大化似然估计或最小化交叉熵损失,训练线性模型的参数。

具体实现原理:

假设逻辑回归为二分类,线性函数为:

\[z = w_1 x_1 + w_2 x_2 + ... + w_n x_n + b\]

其中:

  • \(z\) - 模型的预测值
  • \(x_1, x_2,...,x_n\) - \(n\)个特征变量
  • \(w_1, w_2,...,w_n\) - \(n\)个特征变量对应的模型参数权重
  • \(b\) - 模型的偏置项

将z代入sigmoid函数求概率:

\[p = \frac{1}{1+e^{-z}}\]

其中: p表示输入样本为正类的概率。

则逻辑回归的损失函数为负对数似然或交叉熵。

通过梯度下降算法训练w和b,最小化损失,完成模型。

预测时,计算新样本的概率p,如果p>0.5则预测为正类,否则为负类。

在逻辑回归模型中,常用的损失函数有以下两种:

  1. 对数损失(Log Loss):也称对数似然损失函数,定义为负的对数似然函数,表达式为:

\[Loss = -\frac{1}{N}\sum_{i=1}^N\left[ y_i\log(p_i) + (1-y_i)\log(1-p_i) \right]\]

其中:- \(N\) - 样本数量

  • \(y_i\) - 第\(i\)个样本的真实标签,取值为0或1
  • \(p_i\) - 第\(i\)个样本的预测概率。求和是对所有样本进行遍历。
  1. 交叉熵损失(Cross Entropy):它扩展了对数损失到多分类问题,表达式为:

\[Loss = -\frac{1}{N} \sum_{i=1}^{N} y_{i}\log(p_{i})\]

其中:- \(N\) - 样本数量 - \(y_i\) - 第\(i\)个样本的one-hot编码标签向量 - \(p_i\) - 第\(i\)个样本的预测概率向量

\(y_i\) 是one-hot向量,只有对应真实类别的单个元素值为1。\(p_i\) 是预测概率向量。

\(y_i\log(p_i)\) 计算两个概率分布差异的交叉熵。

求和后取负号得到交叉熵损失。

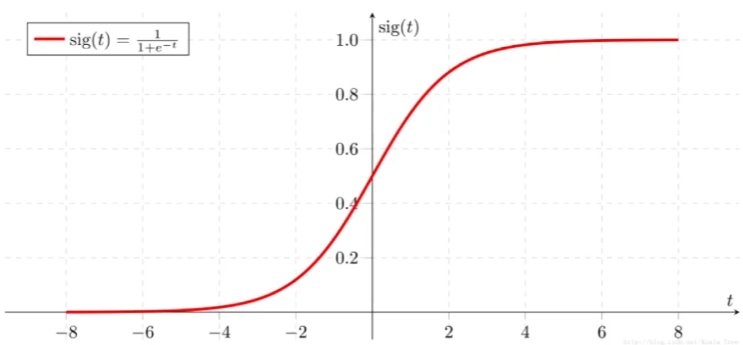
Sigmoid函数的介绍：

Sigmoid函数将任意实数映射到(0, 1)区间内,表达为上述分数形式。

当输入\(z\)趋近正无穷大时,\(e^{-z}\)趋近0,分母趋近1,所以\(p\)趋近1。

当输入\(z\)趋近负无穷大时,\(e^{-z}\)趋近无穷大,分母趋近无穷大,所以\(p\)趋近0。

sigmoid函数的这个S形曲线图形,利用它可以将任意值映射到概率之间,所以常被用作神经网络中门限函数和逻辑回归中概率输出函数。

pCTVfNd.png

抽象的说：逻辑回归=线性回归+Sigmoid函数

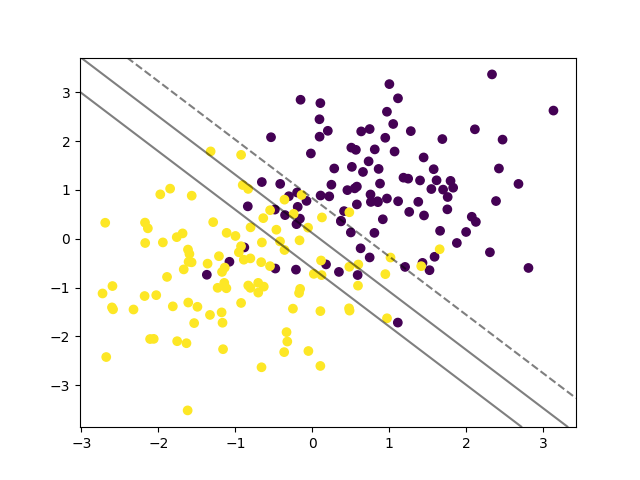
构造两个聚类式的高斯分布数据,用于逻辑回归分类:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import numpy as np
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt

mean1 = [1, 1]
mean2 = [-1, -1]
cov = [[1, 0], [0, 1]] 

X1 = np.random.multivariate_normal(mean1, cov, 100)
X2 = np.random.multivariate_normal(mean2, cov, 100)

X = np.concatenate((X1, X2)) 
y = np.array([0]*100 + [1]*100)

# 训练和预测
clf = LogisticRegression()
clf.fit(X, y) 

# 画出数据分布和决策边界
plt.scatter(X[:,0], X[:,1], c=y)
ax = plt.gca()  
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5)

plt.show()

这里构造了两个高斯分布,分别围绕(1,1)和(-1,-1)生成类0和类1的数据。可以看到逻辑回归学习到了一个合适的决策边界将两个类别尽量分开。

pCTZXqO.png