**SVM(支持向量机)**是一种常用的机器学习算法,主要用于分类问题,但是也可以扩展做回归任务。
SVM的主要思想是:
- 将样本映射到高维空间中,转换为线性可分问题。
- 在高维空间中,存在很多分隔超平面可以将不同类样本完全分开。SVM试图找到这些超平面的最优解,即最大间隔超平面,这样可以获得最佳的分类 GENERALIZATION(泛化)能力。
- 最大间隔超平面可以由支持向量决定,而支持向量就是离分隔超平面最近的样本点。
- 通过核函数,SVM可以隐式地实现高维映射,并建立优化问题求解最大间隔超平面, thus分类模型。
SVM决策超平面的推导过程:
设训练样本为${(x_1, y_1), (x_2, y_2), \cdots, (x_n, y_n)}$,其中$x_i \in \mathbb{R}^d$,$y_i \in {-1,+1}$。
SVM的目标是找到一个分类超平面:
$$w^Tx + b = 0$$
将两类样本完全分开,且间隔尽可能大。
定义样本$x_i$到超平面的函数间隔为:
$$d_i = \frac{|w^Tx_i + b|}{||w||}$$
则求最大间隔等价于最小化$||w||$,满足约束:
$$y_i(w^Tx_i + b) \geq 1, i=1,2,\cdots,n$$
即解决以下优化问题:
$$\min\limits_{w,b} \frac{1}{2}||w||^2$$
$$\text{s.t. } y_i(w^Tx_i + b) \geq 1, i=1,2,\cdots,n$$
引入拉格朗日乘子$\alpha_i \geq 0$,构建拉格朗日函数:
$$L(w,b,\alpha) = \frac{1}{2}||w||^2 - \sum\limits_{i=1}^{n}{\alpha_i[y_i(w^Tx_i + b) - 1]}$$
对$w,b$的偏导数等于0可得:
$$w = \sum\limits_{i=1}^{n}{\alpha_i y_i x_i}$$
$$\sum\limits_{i=1}^{n}{\alpha_i y_i} = 0$$
将$w$代回原问题,得到对偶问题:
$$\max\limits_{\alpha} \sum\limits_{i=1}^{n}{\alpha_i} - \frac{1}{2}\sum\limits_{i,j=1}^{n}{\alpha_i \alpha_j y_i y_j (x_i \cdot x_j)}$$
$$\text{s.t. } \alpha_i \geq 0, \sum\limits_{i=1}^{n}{\alpha_i y_i} = 0$$
求解得到$\alpha$,则最大间隔超平面为:
$$w = \sum\limits_{i=1}^{n}{\alpha_i y_i x_i}$$
$$b = \frac{1}{y_i} - w \cdot x_i, \text{对任一支持向量}i$$
将输入样本映射到高维特征空间。SVM试图在高维空间中找到一个最优分类超平面,以获得最佳的分类效果。
通过核函数实现了从低维到高维的隐式映射。常见的核函数有线性核、多项式核、Gauss核(RBF核)等。
通过求解对偶问题,只需要输入数据的内积,而输入数据的高维映射可以通过核函数实现。
这样就可以在低维输入空间构建最优分隔超平面,而实际上是在高维特征空间实现,从而处理非线性分类问题。
常见的Gauss RBF核将输入映射到无穷维,可以看成在高维空间构建一个泛化能力最强的分类模型。
核技巧扩展了SVM的适用范围,使其不仅适用于线性可分问题,也可用于复杂的非线性分类问题。
通过选择不同的核函数,可以灵活地处理各种类型的数据集。
核技巧是SVM强大的原因之一,它寻求高维映射以求分类的最优解,却只需要计算低维数据的内积, thus有效实现了“维度灾难”的解决。
以下是一个在二维求解决策平面的代码示例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
np.random.seed(0)
X = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]
y = [0] * 20 + [1] * 20
clf = svm.SVC(kernel='linear')
clf.fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100, linewidth=1, facecolors='none',
edgecolors='k')
plt.show()
|

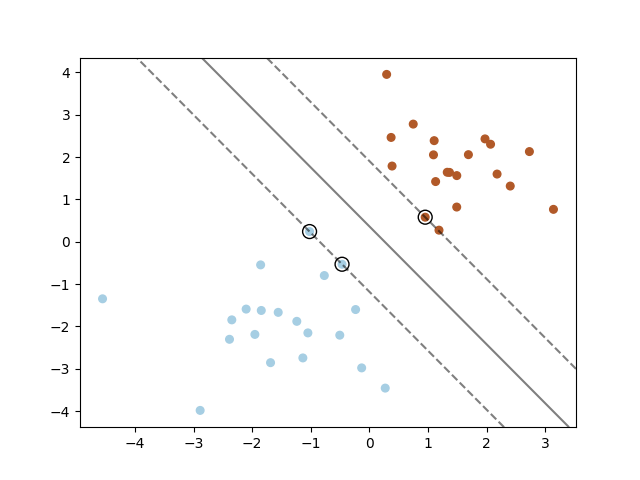
在这个例子中,我们先随机生成了两类二维样本数据,然后训练一个线性核SVM模型,并画出了决策边界。支持向量也被标记出来了。
同样可以求解非线性问题:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
np.random.seed(1)
X = np.vstack((np.random.randn(150, 2) + [1, 2],
np.random.randn(150, 2) - [1, 2]))
y = [0] * 150 + [1] * 150
clf = svm.SVC(kernel='rbf')
clf.fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 200),
np.linspace(ylim[0], ylim[1], 200))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, alpha=0.75, cmap=plt.cm.Paired)
ax.set_xlim(xlim)
ax.set_ylim(ylim)
plt.show()
|

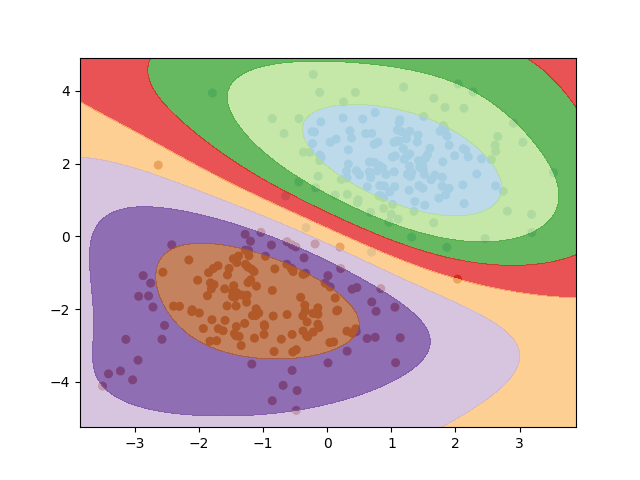
通过构造一个环形分布的二维非线性数据,然后使用RBF核的SVM进行建模。可以看到SVM学会了一个非线性的决策边界将两类不同程度的区分开。
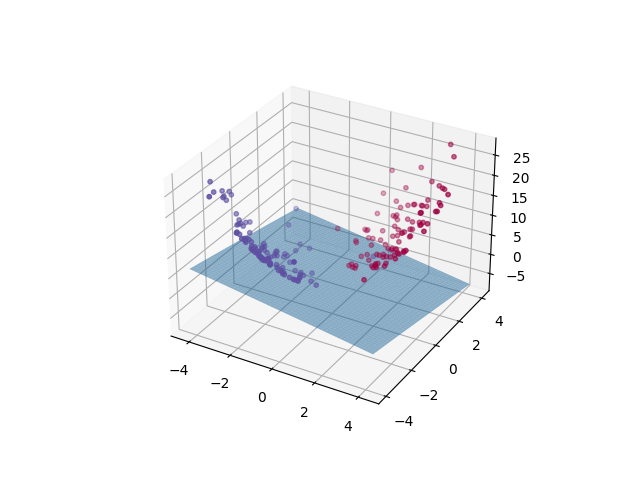
生成了200个样本的二维数据集,然后进行了三维可视化。通过升维操作,SVM可以学习到一个线性的决策面对这些点进行分类。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.svm import SVC
np.random.seed(100)
X1 = np.random.randn(100, 2) + [2, 2]
X2 = np.random.randn(100, 2) - [2, 2]
X = np.vstack((X1, X2)).astype(np.float32)
y = np.array([0] * 100 + [1] * 100)
X_3d = np.hstack((X, (X[:, 0]**2 + X[:, 1]**2)[:, None]))
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X_3d[:, 0], X_3d[:, 1], X_3d[:, 2], c=y, s=10, cmap=plt.cm.Spectral)
clf = SVC(kernel='linear')
clf.fit(X_3d, y)
x1_min, x1_max = X[:, 0].min(), X[:, 0].max()
x2_min, x2_max = X[:, 1].min(), X[:, 1].max()
x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]
x_grid = np.stack((x1.ravel(), x2.ravel(), x1.ravel() ** 2 + x2.ravel() ** 2), axis=1)
y_hat = clf.decision_function(x_grid)
y_grid = y_hat.reshape((200, 200))
ax.plot_surface(x1, x2, y_grid, alpha=0.5)
plt.show()
|

SVM(支持向量机)的主要思想和实现方法可以概括如下:
-
思想:SVM试图找到一个最优分类超平面,使不同类样本 Reality隔的边界尽可能大,从而获得最佳的 GENERALIZATION能力。
-
实现:将样本映射到高维特征空间,转换为线性可分问题。在高维空间中求解最大间隔超平面作为决策面。
-
优化目标:构建约束优化问题,最小化||w||并满足分类约束。求解得到最优w和b确定超平面。
-
对偶问题:引入拉格朗日乘子α,将原问题转换为对偶问题,求解α即可得到最优超平面。
-
核技巧:通过核函数计算输入样本的内积,实现高维映射。常用核有线性核、多项式核、Gauss RBF核等。
-
模型参数:主要就是支持向量及对应的α。决策函数只依赖支持向量。
-
实现方法:一般通过求解相应的凸二次规划问题获得最优α,然后求出w,b。常用SMO算法加速训练。
-
应用:可处理线性和非线性分类问题。还可以扩展到回归任务。
SVM通过间隔最大化寻求最佳分类超平面,核技巧实现高维映射,是一种流行的分类与回归方法。